Page 162 - Fisica per non fisici

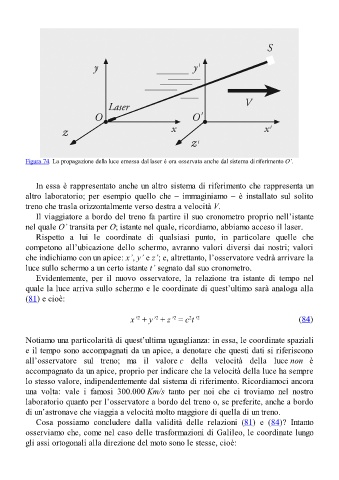
Figura 74. La propagazione della luce emessa dal laser è ora osservata anche dal sistema di riferimento O’.

In essa è rappresentato anche un altro sistema di riferimento che rappresenta un
altro laboratorio; per esempio quello che – immaginiamo – è installato sul solito
treno che trasla orizzontalmente verso destra a velocità V.

Il viaggiatore a bordo del treno fa partire il suo cronometro proprio nell’istante
nel quale O’ transita per O; istante nel quale, ricordiamo, abbiamo acceso il laser.
Rispetto a lui le coordinate di qualsiasi punto, in particolare quelle che

competono all’ubicazione dello schermo, avranno valori diversi dai nostri; valori
che indichiamo con un apice: x’, y’ e z’; e, altrettanto, l’osservatore vedrà arrivare la
luce sullo schermo a un certo istante t’ segnato dal suo cronometro.
Evidentemente, per il nuovo osservatore, la relazione tra istante di tempo nel
quale la luce arriva sullo schermo e le coordinate di quest’ultimo sarà analoga alla

(81) e cioè:

2
2
2
2
x’ + y’ + z’ = c t’ 2 (84)
Notiamo una particolarità di quest’ultima uguaglianza: in essa, le coordinate spaziali
e il tempo sono accompagnati da un apice, a denotare che questi dati si riferiscono
all’osservatore sul treno; ma il valore c della velocità della luce non è

accompagnato da un apice, proprio per indicare che la velocità della luce ha sempre
lo stesso valore, indipendentemente dal sistema di riferimento. Ricordiamoci ancora
una volta: vale i famosi 300.000 Km/s tanto per noi che ci troviamo nel nostro
laboratorio quanto per l’osservatore a bordo del treno o, se preferite, anche a bordo

di un’astronave che viaggia a velocità molto maggiore di quella di un treno.
Cosa possiamo concludere dalla validità delle relazioni (81) e (84)? Intanto
osserviamo che, come nel caso delle trasformazioni di Galileo, le coordinate lungo
gli assi ortogonali alla direzione del moto sono le stesse, cioè: